Intro to Piezoelectric Transducer Crystals
Piezoelectric Materials and Their Properties
Certain single crystal materials exhibit the following phenomenon: when the crystal is mechanically strained, or when the crystal is deformed by the application of an external stress, electric charges appear on certain of the crystal surfaces; and when the direction of the strain reverses, the polarity of the electric charge is reversed. This is called the direct piezoelectric effect, and the crystals that exhibit it are classed as piezoelectric crystals. (See Fig. 1).
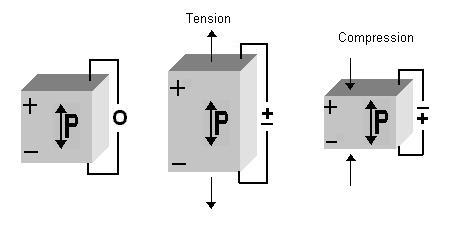
Figure 1. The direct piezoelectric effect.
Conversely, when a piezoelectric crystal is placed in an electric field, or when charges are applied by external means to its faces, the crystal exhibits strain, i.e. the dimensions of the crystal change. When the direction of the applied electric field is reversed, the direction of the resulting strain is reversed. This is called the converse piezoelectric effect. (See Fig. 2).
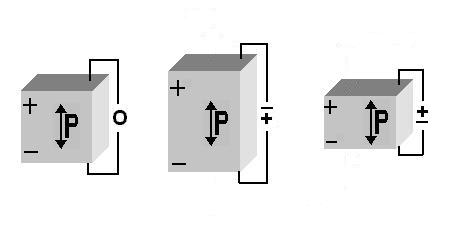
Figure 2. The converse piezoelectric effect.
Piezoelectric Ceramics
Many of today's applications of piezoelectricity use polycrystalline ceramics instead of natural piezoelectric crystals. Piezoelectric ceramics are more versatile in that their physical, chemical, and piezoelectric characteristics can be tailored to specific applications. Piezoceramic materials can be manufactured in almost any shape or size, and the mechanical and electrical axes of the material can be oriented in relation to the shape of the material. These axes are set during poling (the process that induces piezoelectric properties in the material). The orientation of the DC poling field determines the orientation of the mechanical and electrical axes.
Piezoelectric Constants
Piezoelectricity has been demonstrated qualitatively in approximately 1000 crystal materials. These include materials where piezoelectricity occurs naturally, and other single crystal and polycrystalline materials in which piezoelectricity can be induced by the application of high voltage or poling. Typical piezoelectric materials available from Boston Piezo-Optics Inc. are listed in Table 1. In both the direct and converse piezoelectric effects, the strain and stress are related to the electrical parameters by the piezoelectric constants, dij, gij, hij, and eij. These piezoelectric constants have different values for different directions in the material. Furthermore, the stresses and strains are related to each other by the elastic constants of the material in different directions.
| Material | Piezoelectric Constant (10-12 C/N) or (10-12 m/volt) |
Max. Input Voltage (volts/mm) |
Acoustic Power (watts/cm3) (approximate) |
Qm |
|---|---|---|---|---|
| Quartz | d11 = 2.3 d14 = 0.7 | 10500 | 1000 | 2 x 106 |
| Lithium Niobate | d33 = 6.0 d15 = 69.2 | 1000 | 100 | 1 x 105 |
| Navy Type I | d33 = 289 d15 = 496 | 470 | 450 | 500 |
| Navy Type II | d33 = 374 d15 = 584 | 235 | 125 | 75 |
| Navy Tyhpe VI | d33 = 593 d15 = 741 | 235 | 260 | 65 |
| Navy Type III | d33 = 225 d15 = 330 | 470 | 340 | 11 |
| Lead Metaniobate | d33 = 85 | 700 | 85 | 11 |
Table 1. Material Characteristics
Crystal Orienation
The direction in which tension or compression develops polarization parallel to the strain is called the piezoelectric axis.
In quartz, this axis is knows as the "X-axis", and in poled ceramic materials such as PZT the piezoelectric axis is referred to as the "Z-axis". From different combinations of the direction of the applied field and orientation of the crystal it is possible to produce various stresses and strains in the crystal. For example, an electric field applied perpendicular to the piezoelectric axis will produce elongation along the axis as shown in Figure 2. If, however, the electric field is applied parallel to the piezoelectric axis, a shear motion is induced. This type motion is shown in Figure 3.
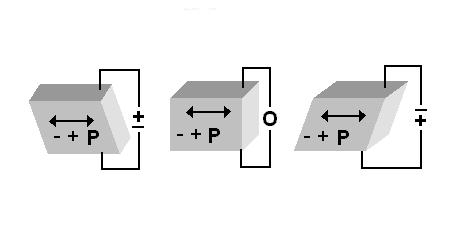
Figure 3. Shear motion
Resonance Frequencies
If, instead of the DC field shown in Figures 2 and 3, an alternating field is applied, the crystal will vibrate at the frequency of the AC field. If the frequency of the AC field corresponds with the frequency where the thickness of the crystal represents half a wavelength, the amplitude of the crystal vibration will be much greater. This is called the crystal's fundamental resonance frequency. The crystal will also have frequencies of large amplitude whenver the thickness of the crystal is equal to an odd multiple of half a wavelength. These are termed harmonic or overtone resonance frequencies (such as 3rd overtone, 5th overtone, etc.). The largest amplitude, however, occurs at the fundamental frequency and as the harmonic number increases the vibration amplitude decreases. A large percentage of energy loss occurs at the two faces of a crystal. For this reason, Boston Piezo-Optics provides overtone polished crystals for use at the higher harmonic frequencies. This specially developed process limits the energy loss, and thereby facilitates the use of higher harmonics (9th overtone, 11th overtone, etc.) and increases the amplitude of all of the resonance frequencies.
The Piezoelectric Constants Defined
It is instructive to take a close look at the meanings of several piezoelectric constants. The most commonly measured of these constants in the piezoelectric strain constant dij. In the longitudinal mode of X-cut quartz, the applicable value is d11. For an applied voltagbe, Vin, d11 will determine the resultant thickness change Δtout or
Δtout = d11 Vin
(Equation 1.)
Equation 1 is only used to interpret the converse piezoelectric effect. To determine the resultant voltage for the direct piezoelectric effect two different piezoelectric constants are used. The piezoelectric constant hij is used to relate the resultant voltage to a given deformation. In this case the thickness change, Δtin, prooduces an output voltage according to
Vout = h11 Δtin
(Equation 2.)
A second constant, the piezoelectric pressure constant gij, is used to relate the resultant voltage to a given applied pressure, P. The resultant voltage Vout is given by
Vout - g11P
(Equation 3.)
Electro-mechanical Coupling Constant
For many applications the material constant of interest is the electro-mechanical coupling factor, kij. This constant is a measure of the piezoelectric material's ratio of output energy to input energy or efficiency.
It is related to the piezoelectric constants according to Equation 4
kij ≈ hijdij
(Equation 4.)
The coupling factor is electrically determined using the resonance frequency data. In Equation 5 the resonance frequency fr and the antiresonance frequency fa are used to determine the widely used thickness mode coupling factor kt. The locations of these two frequencies are depicted for a hypothetical transducer in Figure 4.
kt = Π/2 (fr/fa) Cot Π/2 (fr/fa)
(Equation 5.)
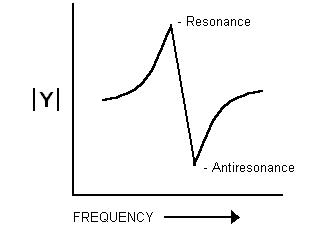
Figure 4. Theoretical Frequency Response
Displacement Amplitude and Output Power
In many instances, it is desirable to know the displacement amplitude and power output of a transducer. Theoretical expressions can be derived for these quantities but they are usually complicated functions involving a number of parameters. Theoretically, piezoelectric plates can be excited to any amplitude of vibration at any frequency, however far from resonance, if the applied voltage is sufficiently high. In practice, however, the maximum power output which can be achieved without damaging the crystal depends on several variables including the type of mounting, frequency, medium, inertia, elastic compliance and internal damping losses of the vibrating crystal itself. These internal losses are a function of the driving frequency. When the operating frequency approaches a resonance, the internal losses sharply decrease and accordingly the amplitude of deformation increases. For high fields, the crystal can suffer dielectric breakdown and mechanical fracture. A resonant voltage which is safe when the transducer is in a liquid or backed by a solid medium may not be safe if the transducer is operated in air. In Table 1, the maximum input voltage for several materials is given. Also given is the approximate maximum acoustic power which is dependant on the input voltage, frequency, electro-mechanical coupling and dielectric properties of the material.
Attenuation and Velocity Measurements
One example of a research use of transducers is to investigate the attenuation and velocity of ultrasonic waves in liquids and solids as a function of comparative parameters. A quartz or lithium niobate transducer is cemented directly to the sample or to a low loss buffer rod made of fused silica, which is in turn cemented to the sample. In this configuration, the transducer is used to both send and receive ultrasound. A signal of known frequency and amplitude is sent out of the transducer and into the sample. From the change in frequency and amplitude detected in the signal that returns to the transducer, the elastic strength and internal damping of the sample is determined. When liquids are being investigated, the transducer or one end of the buffer rod is immersed directly in the liquid.
Using Overtone Resonances
The particular size and frequency of the transducer element to be used depends on the conditions at which one plans to work. For example, a compressional mode PZT-5A transducer, 0.500" in diameter with a 5 MHz fundamental frequency, is approximately 0.0168" thick and can be driven at its odd harmonics to cover a frequency range of 5 to 105 MHz. For higher frequencies up to 1000 MHz, a transducer crystal made from X-cut quartz with a fundamental frequency of 20 MHz (thickness 0.00564") will experience smaller internal losses and is easier to drive at its higher harmonics. Transducers can also be fabricated in the KHz range for low frequency work.
Table 2 indicates the minimum diameter of the transducer to be used at a given frequency with a sample of a given diameter. The desired parallelism of the sample in terms of inches per inch is also given. This table is intended only as a general guide for choosing a suitable transducer. In many experiments it is neither possible nor desirable to obtain a sample to meet the minimum diameter requirements.
| Frequency (MHz) |
Parallelism Constant (in/in) |
Sample Diameter (min. in inches) |
Transducer Diameter (min. in inches) |
|---|---|---|---|
| 1 | 0.0002 | 1.500 | 1.000 |
| 2-5 | 0.0002 | 1.000 | 0.750 |
| 5-10 | 0.0001 | 0.875 | 0.500 - 0.750 |
| 10-100 | 0.00005 | 0.750 | 0.500 |
| 100-200 | 0.00002 | 0.375 | 0.250 |
| 200-1000 | 0.00002 | 0.500 | 0.125 |
Table 2. Size Selection Guide
For coupling a transducer crystal to a sample various materials can be used, such as: conductive and nonconductive epoxy, ceramic cement, and cyanoacrylate glue. For nonpermanent coupling, machine oil, silicon fluid or glycerin can be used. For shear wave transducers, there are commercially available shear wave couplants, and honey will support shear waves as well.
Suggested Reference Material
- "Physical Acoustics", W. P. Mason (Ed.), Academic Press, New York (1964), vol. 1 Part A.2.
- "Piezoelectricity", W. G. Cady, Dover Publications, New York, (1964) and McGraw-Hill Book Co., (1946).3.
- "Precision Frequency Control", E. A. Gerber and A Ballato (Ed.), Academic Press, New York (1985), vol. 1.4.
- "Ultrasonic Transducer Materials", O. E. Mattiat, Plenum Press, London, New York, (1971).5.
- "IEEE Standard of Piezoelectricity", ANSI/IEEE Standard 176-178; Also IEEE Trans. Sonics and Ultrasonics, SU-31, part 2, March 1984.6.
- "Acoustic Waves: Devices, Imaging, and Analog Signal Processing", G. S. Kino, Prentice Hall, Englewood Cliffs, NJ, (1987).
